Сегодня у нас на очереди бинарное дерево (BST), но прежде чем начать вдаваться в детали, предлагаю зайти с практической части и задать вопрос, а зачем?
На мой взгляд самая базовая вещь, в которой нам пригодится понимание BST, это контейнер std::map. Этот контейнер позволяет нам хранить данные в виде ключ — значение, а вариантов применений огромное количество.
Простой пример, нам нужно хранить логин, пароль. Делаем ключ — логин, а значение — пароль. Или у нас есть куча настроек, поступаем также, название настройки ключ, ее величина — значение.
Про то как пользоваться про std::map мы поговорим в другой раз, на текущий момент можно воспринимать мапу как хранилище/базу данных или словарь, где ключ должен быть уникальный, а значение какое угодно
Теперь когда мы понимаем, что мапа это хорошо и удобно, пользоваться ей очень просто, встает вопрос, зачем нам знать про нее что то еще?
И тут самый главный вопрос, это скорость работы, т.е. мы должны понимать, почему в данной ситуации стоит применять этот контейнер или нет. Например, почему мы просто не можем взять массив/вектор элементов, у которого скорость доступа к элементу O(1)?
Вопрос комплексный, всегда нужно учитывать скорость вставки элемента, удаления и доступа. Каждый из контейнеров имеет свои достоинства и недостатки. Поэтому стоит заглянуть под капот и в конце ответить на эти вопросы.
Сразу оговоримся, cppreference говорит, что maps are usually implemented as red-black trees, т.е. реализация мапы может быть какой угодно, но чаще это красно-черное дерево, поэтому для упрощения будем считать, что в нашей ситуации это так.
Теперь вернемся к BST. Обычно в графическом виде его представляют так.
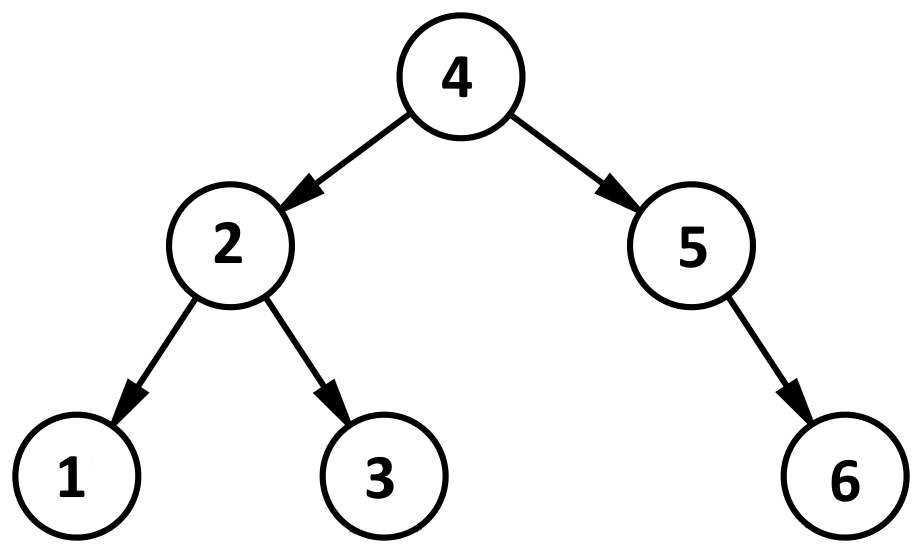
Каждый узел представляет собой такую структуру.
struct TreeNode { int val; TreeNode *left; TreeNode *right; }; |
т.е. у нас есть структура, у которой есть некое значение val. Для упрощения мы рассматриваем тип int, но там может быть и другой тип. Далее имеет два указателя на такую же структуру left и right. Для бинарного дерева характерно то, что если мы пойдем в левую структуру, то там значение val будет всегда меньше нашего val, а для справа всегда будет больше. Ниже картинка, на которой показано для узла 4 и 2 куда ссылаются структуры.
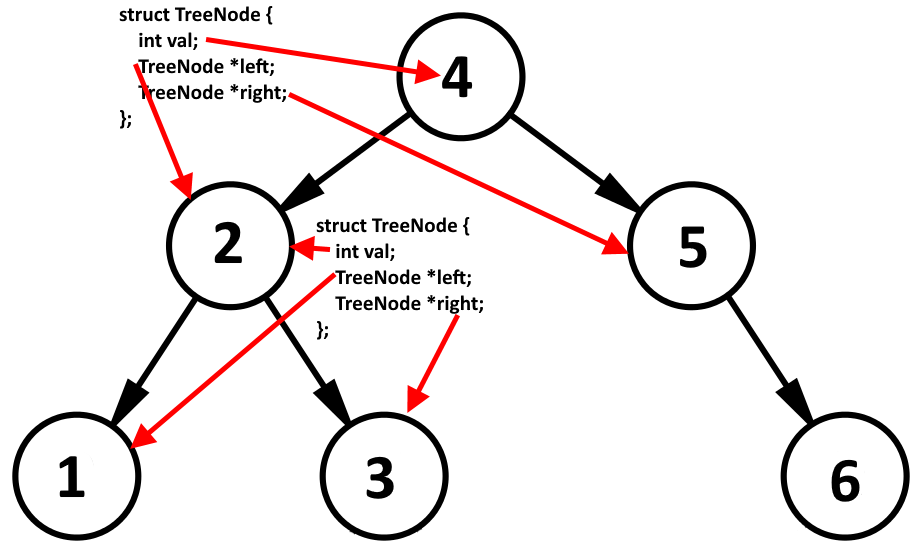
Обычно вершину называют root, а потомков nodes. В чем же плюс BST? Далее начинается магия. Первое как мы сказали ранее, все что левее будет всегда меньше, все что правее будет всегда больше.
Допустим нам нужно обратиться к элементу 3. Начинаем с корня 4, мы точно знаем что 4 больше чем 3, значит наша нода будет где то слева. Переходи на ноду 2 и выясняем что 2 меньше 3, т.е. значение будет где то справа. Идем направо и получаем нужную ноду.
Какие выводы нужно сделать по поводу поиска значения? Изначальный наш набор чисел 1,2,3,4,5,6. Когда мы выяснили что 4 больше чем 3, то отсекли из поиска половину набора, т.е. у нас осталось 1, 2, 3. После того как сравнили 2 и 3, то исключили еще половину значений, т.е. осталось только 3. Подобная сложность называется log n, т.е. каждый раз мы искали в половине от половины.
Вывод номер один, поиск в бинарном дереве занимает log n времени. Если бы мы искали 3 в том же не отсортированном массиве 1,2,6,4,5,3, я умышленно поставил 3 в конец, то в худшем случае нам пришлось бы сравнить 1 и 3, 2 и 3, 6 и 3, т.е, сделать 6 сравнений прежде чем нужная тройка бы нашлась. В случае с бинарным деревом, нам понадобилось 3 сравнения чтобы найти искомую величину.
Тоже самое касается и вставки элемента и удаления. Но всегда ли это так? Увы нет, тут есть некоторый обман. Допустим у меня есть только корневая нода 6, вставляем ноду 5, где она окажется? Правильно слева. Вставляем ноду 4, идем налево от 6, потом налево от 5. Вставляем. Далее по аналогии вставляем 3, 2, 1. В итоге у нас получается такая вот картинка.

И что же вышло? Увы но получилось, что для вставки нам потребовалось O(n) операций, т.е. выигрыша никакого не получилось. Поэтому когда мы говорим про операции вставки, удаления и поиска, то для бинарного дерева в худшем случае это O(n), а в среднем O(log n)
Чтобы избежать подобных ситуаций, применяют балансировки деревьев, но отдельная тема и об этом мы поговорим в другой раз
Еще одна картинка, которая мне очень нравится, которая помогает понять идею BST.
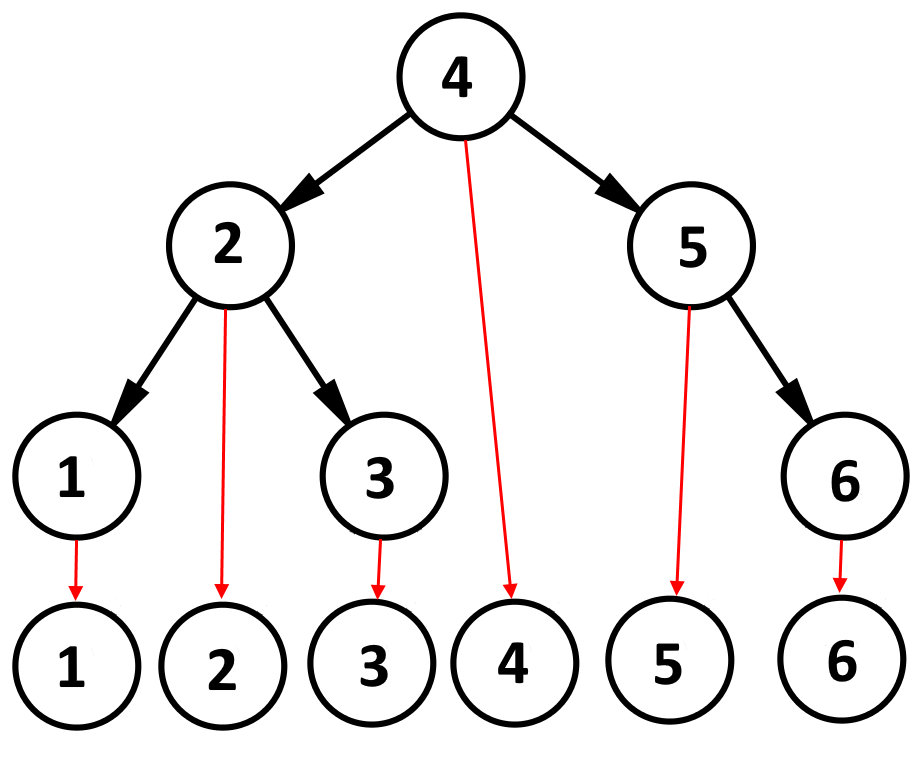
И что мы видим? Если ноды опустить вниз, то мы получим отсортированный список. Но как нам это поможет? Дело все в том, что при определенном обходе дерева, мы можем получать отсортированные данные.
И тут мы плавно подходим к мысли о том, как вообще обойти все дерево. Тут есть два основных подхода, DFS — обход в глубину и BFS обход в ширину.
DFS довольно таки легко реализуется с помощью рекурсии. Первое что надо знать про рекурсию, это то что из нее должен быть выход, иначе мы словим ситуацию, когда функция будет вызвать сама себя бесконечно. Далее смотрим на кодяру и пытаемся ее применить к нашему дереву 1,2,3,4,5,6.
void DFS(TreeNode* root) { if(root == nullptr) return res; if(root->left != nullptr) { DFS(root->left); } if(root->right != nullptr) { DFS(root->right); } } |
Шаг 1. заходим в функцию, root указывает на 4, поэтому идем мимо проверки что нода существует и подходим к проверке существует ли левая нода. Существует. На этом моменте мы снова вызываем эту же функцию, но от ноды слева root->left.
Шаг 2. Теперь наш root это 2. Снова повторяем действия выше и снова идем налево
Шаг 3. root 1. Те же действия, что и выше, идем в налево
Шаг 4. root теперь null, а это значит что мы выходим из рекурсии и оказываемся в этой точке:
void DFS(TreeNode* root) { if(root == nullptr) return res; if(root->left != nullptr) { DFS(root->left); /// <------------ мы только что вышли отсюда, при этом root это 1 } if(root->right != nullptr) { DFS(root->right); } } |
Мы наконец то вышли из первой из функций root->left. root в данной точке 1. Теперь нам нужно сходить направо от 1, но так как справа у нас тоже null, то мы выходим из функции, когда root был 1.
Шаг 5. Выскакиваем в точку когда root был 2. Теперь мы сходим направо от 2. Там сходим слева и справа от 3. И снова поднимемся на уровень 4.
Шаг 6. Аналогичным будет обход справа от 4, т.е. сначала посещаем все левые ноды, а затем правые.
Если внимательно посмотреть на данный код, то можно заметить одну особенность, мы всегда сначала идем влево, а потом направо, но очень важно в какой момент мы будем обращаться к данным. Возьмем для примера вектор vector<int> res в который будем помещать числа.
Вариант номер 1.
vector<int> res; void DFS(TreeNode* root) { if(root == nullptr) return res; if(root->left != nullptr) { res.push_back(root->val); DFS(root->left); } if(root->right != nullptr) { DFS(root->right); } } |
Т.е. мы сначала будем добавлять число, а потом заходить в рекурсию. На выходе мы получим вектор из чисел 4, 2, 1, 3, 5, 6. Такой порядок называет Pre-order. Итого, мы будем опускаться сверху вниз налево, потом обойдем внизу справа и будем подниматься, а затем только пойдем в правую часть дерева.
vector<int> res; void DFS(TreeNode* root) { if(root == nullptr) return res; if(root->left != nullptr) { DFS(root->left); } if(root->right != nullptr) { DFS(root->right); } res.push_back(root->val); } |
Такой порядок называется Post order. 1,2,5,6,4. В этом случае мы будем добавлять сначала нижние ноды слева и справа, а затем подниматься к верху, т.е. root будет в самом конце
Ну и самый интересный вариант обхода это In order, т.е. сначала мы опустимся в самый низ и обойдем все левые ноды, а затем только правые. Если внимательно посмотреть, то в этом случае мы получим отсортированный список.
vector<int> res; void DFS(TreeNode* root) { if(root == nullptr) return res; if(root->left != nullptr) { DFS(root->left); res.push_back(root->val); } if(root->right != nullptr) { DFS(root->right); } } |
Для желающих предлагаю опробовать решения на leetcode:
144. Binary Tree Preorder Traversal
145. Binary Tree Postorder Traversal
94. Binary Tree Inorder Traversal
Рекурсия не единственный способ решения для DFS, но самый простой для понимания
Кроме обхода в глубину, есть еще способ обхода в ширину BFS, т.е. мы идем слоями, сверху вниз.
int BFS(TreeNode* root) { queue<TreeNode*> q; q.push(root); while(!q.empty()) { TreeNode* node = q.front(); //берем текущую ноду из очереди q.pop(); //убираем ее из очереди if(node->left) //проверяем есть ли потомки слева q.push(node->left); //добавляем их в очередь if(node->right) //проверяем есть ли потомки справа q.push(node->right); //добавляем их в очередь } } |
Шаг 1. Добавили в очередь root. Пошли в цикл проверять, кто в очереди, там 4, у него есть потомки 2 и 5, добавляем их в конец очереди и убираем 4, т.к. ее обработку закончили.
Шаг 2. В очереди 2, в конец добавляем ее потомков 1 и 3, выкидываем 2.
Шаг 3. Пришло время 5, у нее потом 6, добавляем в конец.
Шаг 4. Спускаемся на уровень ниже, обрабатываем слева направо 1, 3 и 6.
Итого получается такая вот картинка

Итого, что мы должны были вынести из этой статьи. Нас интересует в первую очередь мапа, это очень популярный контейнер для данных. Как хороших программистов нас должно интересовать можно ли использовать мапу в конкретно нашем случае, устроит ли нас скорость log n? Нужны ли нам данные отсортированные?
Далее мы заглянули под капот мапы и узнали про бинарное дерево поиска, как оно устроено и как работает. Знания про bst могут быть так же использованы для сортировки данных или например в таком контейнере как priority queue
На закуску предлагаю посмотреть возможный код решения задач с leetcode
1302. Deepest Leaves Sum Medium Given the root of a binary tree, return the sum of values of its deepest leaves. Найти сумму самых нижних нод/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: int level; //переменная в которой храним текущий уровень int sum; //переменная в которой храним сумму текущего уровня int deepestLeavesSum(TreeNode* root) { level = 0; sum = 0; deepestLeavesSum(root, 0); //заходим в рекурсию на уровень 0 return sum; } void deepestLeavesSum(TreeNode* root, int val) { if (root == nullptr) return; if(val == level) //если текущий уровень такой же то просто добавляем к сумме величину текущей ноды { sum += root->val; } else if (val > level) //если уровень глубже тех что были раньше, то обновляем уровень и заново инициализируем сумму. { level = val; sum = root->val; } deepestLeavesSum(root->left, val + 1); //переходим на уровень ниже слева deepestLeavesSum(root->right, val + 1); //переходим на уровень ниже справа } }; |
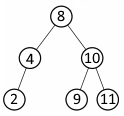
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { private: int helper(TreeNode* root) { int total = 0; if(root->left) { total += root->left->val; } if(root->right) { total += root->right->val; } return total; } public: int sumEvenGrandparent(TreeNode* root) { queue<TreeNode*> q; q.push(root); int total = 0; while(!q.empty()) { TreeNode* cur = q.front(); //берем текущую ноду из очереди q.pop(); //убираем ее из очереди if(cur->left) //проверяем есть ли потомки слева { q.push(cur->left); //добавляем их в очередь if(cur->val % 2 == 0) total += helper(cur->left); //вызываем обработчик для потомка слева } if(cur->right) //проверяем есть ли потомки справа { q.push(cur->right); //добавляем их в очередь if(cur->val % 2 == 0) total += helper(cur->right); //вызываем обработчик для потомка справа } } return total; } }; |


Добавить комментарий